

ACTIVIDADES CON EL GEOPLANO
FÓRMULA DE PICK
1.- Un Geoplano, en su versión original, es un tablero con una malla de clavos. En él se pueden formar figuras utilizando gomas elásticas. Nosotros vamos a trabajar en un ciber-geoplano 5x5, es decir una malla cuadrada de 25 puntos como puedes ver en la figura. Todas las figuras geométricas que construyas deben tener sus vértices en puntos de la malla. Consideraremos que dos figuras son distintas si no son congruentes. Se toma como unidad de superficie el cuadrado mínimo de la malla.
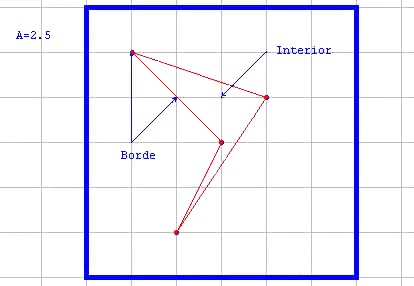
En las actividades siguientes vas a tener que contar los puntos interiores y los puntos en el borde de los polígonos que construyas. En la figura que sigue hay un cuadrilátero con 5 puntos en el borde (los puntos de la malla que están en los lados del cuadrilátero) y un punto interior (los puntos de la malla que están dentro del cuadrilátero).
Arriba a la izquierda tienes el área del cuadrilátero, este valor lo da automáticamente el programa, pero es un buen ejercicio el que lo halles por ti mismo. Para esto sólo tienes que recordar como se calcula el área de un triángulo, el área de un paralelogramo y quizá el área de un trapecio.
¡ Empezamos !.Utilizando la siguiente escena realiza las actividades:
a) Forma 10 triángulos distintos y haz una tabla como la siguiente en tu cuaderno:
|
Triángulo 1 |
Triángulo 2 | Triángulo 3 | Triángulo 4 | Triángulo 5 | Triángulo 6 | Triángulo 7 | Triángulo 8 | Triángulo 9 | Triángulo 10 | |
| Puntos en el interior | ||||||||||
| Puntos en el borde | ||||||||||
| Área |
b) Encuentra todos los triángulos rectángulos distintos posibles ( hay 17 ). Como ayuda tienes la siguiente tabla:
![]()
El primer número es el área y entre paréntesis los triángulos que hay con esa área. Cuando no hay número entre paréntesis es que sólo hay uno.
c) Podrías formar un triángulo equilátero.
2.- Vamos a trabajar ahora con figuras de cuatro lados:
a) Encuentra todos los cuadrados distintos posibles ( Hay 8).
b) Encuentra todos los rectángulos distintos posibles ( Hay 8).
Con las 16 figuras haz la tabla:
|
Cuadrado 1 |
Cuadrado 2 | Cuadrado 3 | ... | Cuadrado 8 | Rectángulo 1 | Rectángulo 2 | ... | Rectángulo 8 | |
| Puntos en el interior | |||||||||
| Puntos en el borde | |||||||||
| Área |
c) Encuentra todos los paralelogramos distintos. A parte de los 8 cuadrados y de los 8 rectángulos, puedes formar 26 paralelogramos. Como ayuda tienes los siguientes datos:
![]()
Como antes, el primer número es el área y entre paréntesis los paralelogramos que hay con esa área. Cuando no hay número entre paréntesis es que sólo hay uno.
d) Puedes observar que no se pueden formar en la malla paralelogramos ( no rectángulos) de área 10 y 11.¿Podrías explicar por qué?
e) Forma 5 cuadriláteros distintos, sin que los lados se corten, que no sean paralelogramos y haz de nuevo la tabla:
|
Cuadrilátero 1 |
Cuadrilátero 2 | Cuadrilátero 3 | Cuadrilátero 4 | Cuadrilátero 5 | |
| Puntos en el interior | |||||
| Puntos en el borde | |||||
| Área |
3.- Experimenta formando polígonos, sin que los lados se corten, con 5, 6 y 7 lados. Con las figuras que formes haces de nuevo la tabla:
|
Polígono 1 |
Polígono 2 | Polígono 3 | Polígono 4 | Polígono... | |
| Puntos en el interior | |||||
| Puntos en el borde | |||||
| Área |
4.- Fórmula de Pick y más ejemplos.
a) Con todos los datos obtenidos en las actividades anteriores,¿podrías sacar una relación entre los puntos interiores, los puntos en el borde y el área de un polígono?
La fórmula la descubrió G. Pick en 1899.
b) Experimenta por tu cuenta en el ciber-geoplano 10x10 siguiente. Anota en tu cuaderno los resultados obtenidos.
5.-Compliquemos las cosas
Si te fijas en la figura siguiente, un cuadrado con un agujero, puedes observar que la fórmula de Pick no funciona. Experimenta con diversas figuras con un agujero e intenta relacionar los puntos interiores, los puntos en el borde, el área y el agujero.
Autor: Carlos Maroto Bañares